هندسه زیباست
در نظر دارم موضوع علم دقیق و بیان هندسه به عنوان یک علم دقیق را مطرح نمایم. در حقیقت بیان این مطلب برای مطرح نمودن موضوع عقیده در آینده نیاز است.
قبل از شروع بحث ضروری می دانم نامه ای را که توسط یکی از خوانندگان در مبحث گفتمان برایم رسید در اینجا بیاورم. ایشان نوشته است که:
«من از کلاس پنجم ابتدایی از مدرسه در سال ۱۳۵۶ اخراج شدم دلیل اخراج توهین غیرقابل بخشش معلم احمقی بود که نگاه ضد دینی و سیاسی خودش را با کینه به من که مرحوم پدرم که یک روحانی بود با توهینهای بسیار زشت و مسخره کردن من در کلاس جلوی همکلاسیهام بود، تخلیه می کرد. یک روز از من خواست که مسئله ریاضی را که بر اساس توهین به پدرم مطرح کرده بود، حل کنم و من انجام ندادم و شروع کرد به ضرب و شتم من. در این درگیری آن فرد نادرست به زمین خورد و موجب خنده بچه‌ها شد و من اخراج شدم تا این که با وساطت و اصرار بسیار فراش مدرسه که اهل زارچ بود بالاخره قبول کردند فقط در امتحانات نهایی شرکت کنم و با معدل پایین قبول شدم و بعد از آن پدرم در ۱۱ سالگی من و برادرم رو به حوزه برد تا این که پس از چند سال به اصرار یک معلم که هنوز با هم دوستیم به ادامه تحصیل و البته غیرحضوری که آن وقتها متفرقه گفته می شد، پرداختم. روزگار مشکلی بود. باید خودم درس می خواندم و پایان سال امتحان می‌دادم خلاصه با هر زجری بود دیپلم ریاضی گرفتم و البته با معدل ۱۴ و دوباره به توصیه همان معلم امتحان کنکور دانشگاه آزاد در رشته فیزیک دادم که چون در شهر خودمان بود با هر زحمتی ادامه دادم حالا درس حوزه بود خرج دانشگاه آزاد که فکر کنم ترمی ۱۱ هزار تومان می‌شد مجبور بودم کارگری آهنگری اسکلت ساختمان کنم تا هزینه ادامه را داشته باشم در این مسیر با دکتر محمود بهار مترجم هالیدی آشنا شدم که بیشتر دوست بود تا مدرس، وقت زیادی برایم می‌گذاشت و من بیشتر روی مفاهیم فیزیک با ایشان بحث می کردم، خوشحال بودم که یک پارادایم برایم پیش آمده بود … »
دقت کنید که مشکلات ایشان که قبل از انقلاب شروع شده بود بعد از انقلاب نیز ادامه پیدا کرده بود.
قبلاً در رابطه با روشهای علمی این مطلب را مطرح کردم که دو روش موجود است. یکی روش تشریحی و دیگری روش دقیق هستند.
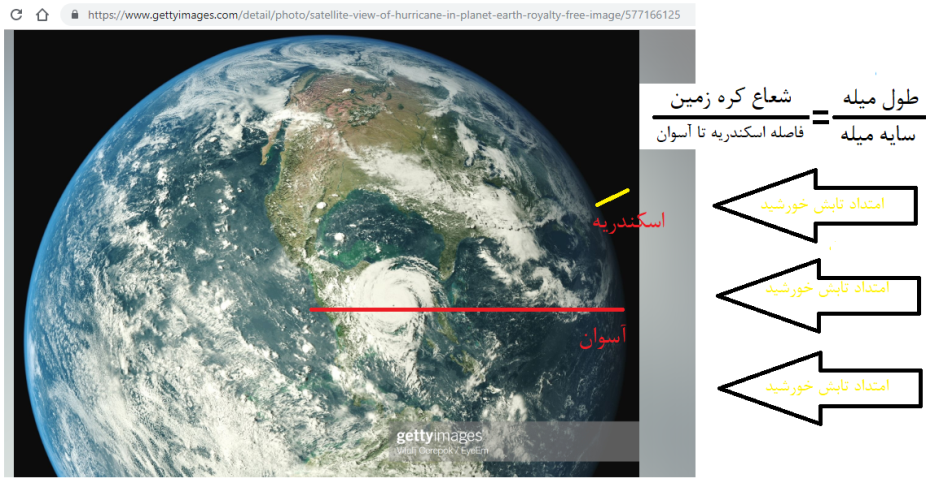همه علوم از ابتدا به روش تشریحی مطرح و بحث می شدند. در روش تشریحی برای اثبات یک موضوع ضروری است که تعدادی (جمعیتی) را جهت آزمون انتخاب کنند. در رابطه با این جمعیت مطلبی مورد آزمایش یا تحقیق قرار می گیرد. به روش آماری موضوع مورد بحث را نتیجه می گیرند. در تمدن (سه هزار ساله) مصر، علم هندسه ابزار علمی و ریاضی مطرح بود. تمام ساختمانها و آنچه از آن دوران مانده است در چارچوب هندسه مسطحه بوده است. آنها اعتقاد داشتند که زمین به شکل کره است (دقت کنید که چند هزار سال بعد کلیسا از گالیله اقرار می گیرد که زمین کره نیست) و با استفاده از هندسه شعاع کره زمین را اندازه گرفتند. روش مصری ها برای اندازه گیری شعاع کره زمین را در شکل آورده ام. آنها در شهر آسوان چاهی را کنده بودند. (خط قرمز در شکل شعاع کره زمین که به شهر آسوان می رسید و محلی که چاه حفر شده بود است.) آسوان در منطقه حاره است. در آسوان در طول سال دو روز آفتاب دقیقا عمود بر سطح زمین می تابد. برای اینکه مطمئن باشند آفتاب بر سطح زمین عمود است، چاهی در آسوان کنده بودند.
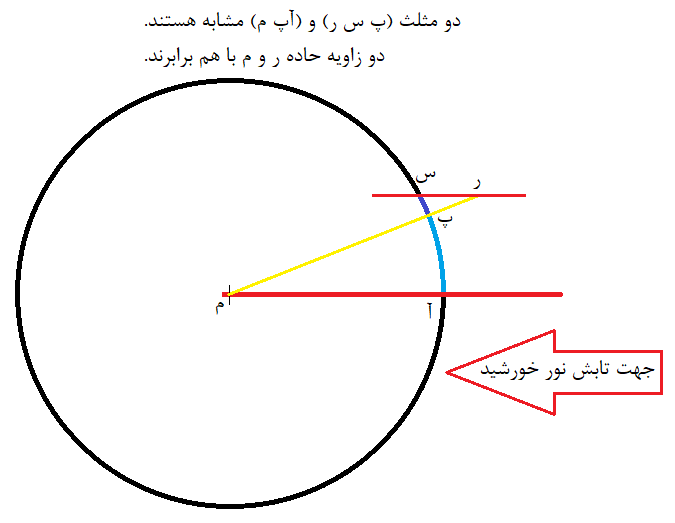زمانی که نور آفتاب به ته چاه می رسید، اندازه سایه میله ای که در اسکندریه عمود بر زمین برقرار شده بود را به دست می آوردند. (در شکل خط زرد نشانه میله در شهر اسکندریه است.) طبق رابطه ساده در شکل شعاع کره زمین به دست می آمد. در حقیقت آنها از دو قضیه هندسه استفاده کرده بودند که در شکل دیگر نشان داده ام.
قضیه اول: اگر خطی رسم کنیم که دو خط موازی را قطع کند، دو زاویه کوچک (حاده) و دو زاویه بزرگ (منفرجه) ایجاد شده برابرند.
بر اساس این قضیه، در این مسئله دو زاویه «ر» و «م» در شکل برابرند.
قضیه دوم: دو مثلث قائم الزاویه که یکی از زوایای حاده آنها برابر باشند با هم متشابه اند. و در نتیجه نسبت اضلاع مشابه آنها با هم برابرند.
در این مسئله دو مثلث «پ س ر» و «آپ م» تقریباً با هم مشابه هستند. دقت کنید نوشتم تقریباً با هم مشابه هستند. یعنی مصری ها این موضوع تقریباً را هم می شناختند. البته به دلیل اینکه نسبت طول میله و شعاع کره زمین عدد خیلی کوچکی هست، این تقریب مناسب است. و جوابی که برای شعاع کره زمین به دست آورده اند با آنچه امروز می دانیم خیلی نزدیک است. باید بگویم که نسبت به ابزاری که داشته اند خیلی خوب بوده است.
موضوع اصلی این که مصریها دو قضیه بالایی را به روش تشریحی ثابت می کردند.
مثلا برای قضیه «اگر خطی رسم کنیم که دو خط موازی را قطع کند، دو زاویه کوچک (حاده) و دو زاویه بزرگ (منفرجه) ایجاد شده برابرند.» به روش تشریحی نیاز بود که تعداد زیادی خط موازی رسم کنند و دو زاویه حاده بین آن دو را اندازه بگیرند. براساس این مطالعه آماری نتیجه می گرفتند که دو زاویه با هم برابرند.
به همین ترتیب برای اثبات قضیه «دو مثلث قائم الزاویه که یکی از زوایای حاده آنها برابر باشند با هم متشابه اند. و در نتیجه نسبت اضلاع مشابه آنها با هم برابرند.» با رسم تعداد زیادی مثلث قائم الزاویه که یکی از زوایای حاده آنها برابر بود، نسبت اضلاع را به دست می آوردند و نتیجه می گرفتند که این قضیه درست است.
اما هندسه در روش دقیق کاملاً متفاوت است.
یونانی ها (اقلیدس اسکندریه) 2300 سال قبل هندسه ای که پایه و اساسش در مصر بود از یک علم تشریحی به یک علم دقیق در آوردند. دقت کنید اقلیدس به نام اقلیدس اسکندریه معروف است. اقلیدس دیگری در یونان و قبل از او بود. هندسه به عنوان یک علم دقیق به این صورت است که:
– فرضهای اولیه دارد که لازم است بدون دلیل بپذیریم.
– قضایایی دارد که بدون اثبات باید آنها را بپذیریم. لذا به آن اصل می گوییم.
(گریزی بزنم به موارد اجتماعی: ما در قانون اساسی اصل داریم ولی در قوانین عادی ماده و بند و تبصره و نظایر آن داریم.)
– کمیاتی داریم که بر پایه فرضهای اولیه تعریف می شوند.
– قضایایی داریم که براساس اصل (اصلهایی که پذیرفته ایم) و قضایای اثبات شده قبلی اثبات می کنیم.
در هندسه فرضهای اولیه عبارتند از:
– در یک صفحه می توان تنها یک خط مستقیم از یک نقطه به یک نقطه دیگر رسم کرد.
– در یک صفحه می توان یک پاره خط (خط محدود) را می توان به طور پیوسته به صورت تنها یک خط از هر دو طرف ادامه داد.
– در یک صفحه از هر نقطه با اندازه شعاع مشخصی تنها یک دایره می توان رسم کرد.
– تمام زوایای قائمه (90 درجه) با هم برابر هستند.
– همه اجسام هندسی که با یک جسم هندسی برابرند با هم دیگر برابر هستند.
– اگر جسمی را به دو جسم برابر جمع ببندیم دو جسم برابر دیگر به دست می آیند.
– اگر جسمی را از دو جسم برابر کم کنیم دو جسم برابر نتیجه می شود.
– اگر دو یا چند جسم هندسی برهم منطبق شوند همه آن ها با هم برابرند.
– کل از هر جزء بزرگتر است.
اصول در هندسه اقلیدسی:
اصل خطوط موازی: اگر خط راستی دو خط راست دیگر را به گونه ای قطع کند که زوایای ایجاد شده در یک طرف خط راست اول مجموعاً کمتر از دو زاویه قائمه باشند، دو خط راست نهایتاً در همان طرف هم دیگر را قطع می کنند.
اثبات یک قضیه:
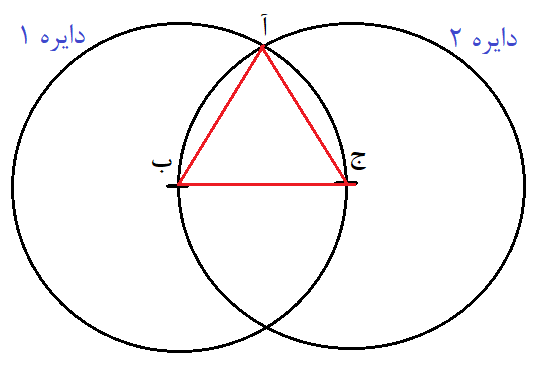قضیه: مطابق شکل دو دایره به شعاعهای مساوی رسم می کنیم به گونه ای که مرکز یکی منطبق بر محیط دیگری است. مثلث رسم شده (آ ب ج) یک مثلث متساوی الاضلاع است.
اثبات:
سه ضلع مثلث (آ ب ج) با هم برابرند چونکه شعاعهای دایره هستند. پس این مثلث متساوی الاضلاع هست.
در این هفته موضوع هندسه اقلیدسی را به عنوان یک علم دقیق مطرح کردم تا بعداً بتوانم نشان بدهم که حل مسائل فرهنگی با راهها و مدلهای ساده حل شدنی است.
هندسه اقلیدسی تا زمانی که نیوتون مکانیک را به صورت یک علم دقیق مطرح کرد از این نظر تنها بود. به عبارتی دیگر تا آن زمان هندست تنها علم دقیق بود. بعداً هندسه های دیگری و شاخه های دیگر فیزیک و شاخه های دیگر ریاضی به صورت علم دقیق مطرح شده اند.
در علوم دقیق می توان زیبایی خاصی دید. هر علمی که به صورت دقیق مطرح می شود به نوعی زیباست. این زیبایی زمانی افزوده می شود که تعداد اصول یک علم دقیق کمتر باشد.
هندسه اقلیدسی اولین علم زیبای بنا نهاده شده توسط انسان است.
در فرهنگ هم هرگاه مقدار اصول افزایش یابد از زیبایی کاسته می شود.